Computational modeling of bilayer membranes

One of the factors limiting the size of membranes in computer simulations is the large number of solvent molecules which fill the simulation cell. We have recently developed a novel computer model of bilayer membranes in which the membranes are simulated without the embedding solvent as if they were in vacuum. The lipids are modeled as trimers with pair-interactions that implicitly account for the hydrophobic effect. Using this new model we have been able to investigate the behavior of large membranes containing 1000 lipids. Despite its conceptual simplicity, the model reproduces many common features of bilayer membranes, such as a solid-fluid phase transition, pore formation, and trans-bilayer diffusion (flip-flop). Its unusual efficiency makes simulations of membranes consisting of thousands of molecules feasible - much above the capability of atomistic and other coarse-grained models where solvent is modeled explicitly. This makes the model an excellent tool for testing concepts and theories on the mesoscopic scale.

Figure: Equilibrium configuration of a fluid membrane consisting of 1000 molecules (500 molecules in each monolayer).

Statistical-mechanics of fluctuating surfaces

Many monolayer and bilayer systems are frequently assumed to be saturated, i.e., having a nearly-vanishing surface tension. The reason for this assumption is the fact that the energy required to change the area density of the constituent amphiphilic molecules is much larger than the thermal and curvature energies. Consequently, the effect of area elasticity (also known as Schulman elasticity) on the stretching behavior of fluctuating bilayers has been very little investigated. We have studied this issue using a statistical-mechanical model including both the Schulman and curvature (Helfrich) energies. Our model clarifies that elasticity of surfaces is determined by an interplay between the Schulman elastic energy, curvature elasticity, and entropy. Our theoretical results agree with micropipet aspiration measurements of giant unilamellar vesicles.

In another study we used a statistical mechanical analysis to derive virial expressions for the elastic coefficients of fluctuating surfaces (surface tension, bending and Gaussian-curvature moduli), relating them to the microscopic potentials and the distribution functions of the molecules. We used these expressions to compute the elastic coefficients of our computer-model membrane. The numerical values of the elastic coefficients which we obtain from these expressions are in agreement with the values extracted from a spectral analysis of the thermal fluctuations.

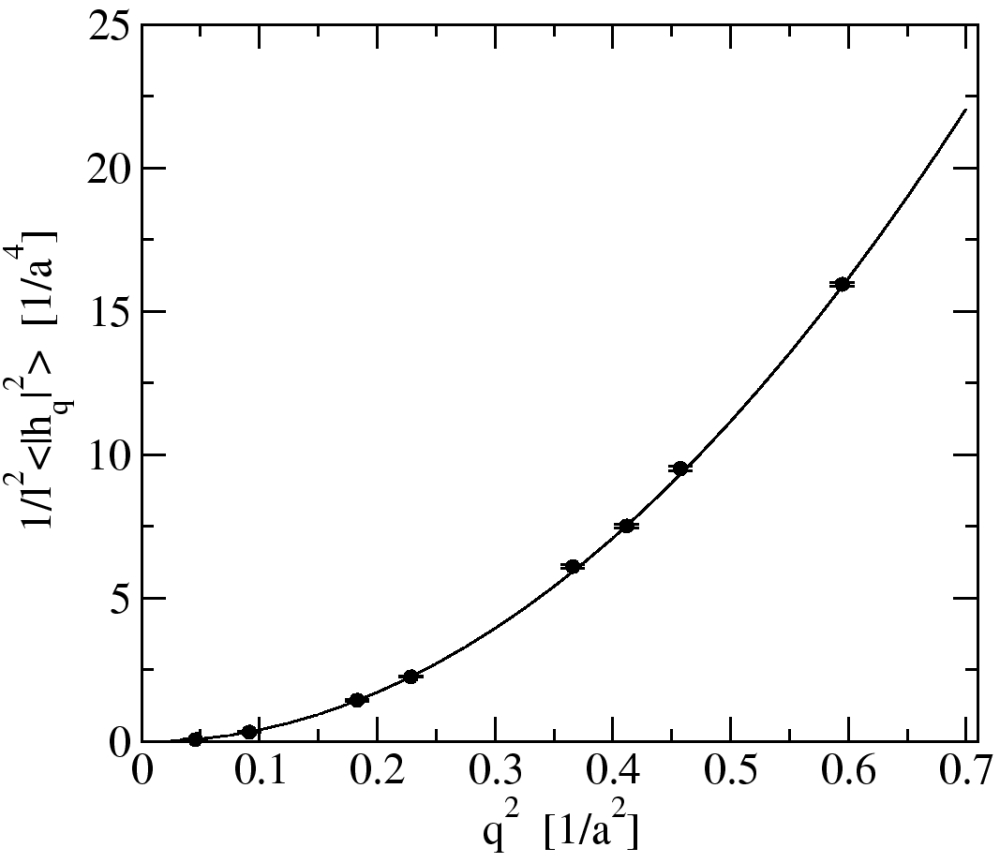
Figure: The inverse of the spectral intensity for undulatory modes as a function of the square wave number.

Pulling knotted polymers

The static and dynamic behavior of single polymer chains (e.g., DNA) and multichain systems (e.g., gels and rubber) is strongly influenced by knots and permanent entanglements. In this work we used Monte Carlo simulations to compare the force-extension relations of knotted and unknotted self-avoiding chains of several sizes. The results of the simulations of unknotted chains could be easily explained using simple scaling arguments. By contrast, knotted polymers exhibit strong finite size effects which can be interpreted in terms of a new length scale related to the size of the knot. Based on this interpretation, we have extracted the scaling dependence of the mean knot size on the length of the polymer.

Figure: Two configurations of a knotted chain of 335 bonds. The (grey) knotted regions consist of 112 (top) and 32 (bottom) bonds.

Entropic elasticity of soft-matter systems

Systems of hard spheres tethered by inextensible bonds can be used to model real soft matter systems whose thermodynamic properties are determined by entropy rather than energy, like colloids and polymeric gels. We have developed a method well suited for numerical calculation of the elastic constants of such model systems, and demonstrated its efficiency and accuracy on several systems. One of the interesting problems which we addressed is related to the elastic behavior of percolation networks near the sol-gel transition. We found (both in two- and three-dimensions) that the shear modulus of such networks has a power-law dependence on the distance from the percolation threshold, with a characteristic exponent that is similar to the conductivity exponent of random resistor networks. This result thus "closes a circle" which began more than twenty years ago, when it became clear that the analogy between the (entropic) gel elasticity and conductivity proposed by de Gennes, is far from being obvious.

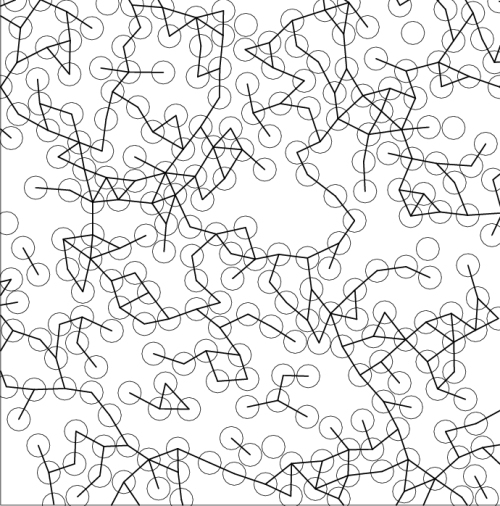
Figure: Equilibrium configuration of 2D percolation system consisting of hard spheres and inextensible tethers.