Lubricated gravity currents and the genesis of ice streams
 |
The motion of glaciers over their bedrock or drops of fluid along a solid surface can vary dramatically when these substrates are lubricated. We investigate the coupled flow of a gravity current (GC) of strain-rate softening fluid that is lubricated by a denser, lower-viscosity Newtonian fluid. We present a set of experiments in which such GCs were discharged axisymmetrically and at constant flux over a flat surface. Using imaging techniques we follow the evolution of the front and thickness field of each fluid. We find that, unlike purely Newtonian lubricated GC, the fronts of the non-Newtonian and lubricating Newtonian fluids have power-law time evolution with different exponents. Each of these exponents is similar to that of a non-lubricated GCs of the same fluid. Nevertheless, the fronts of our lubricated GCs evolved faster than those of the corresponding non-lubricated GCs due to larger intercepts. In addition, in contrast with the monotonically declining thickness of non-lubricated GCs, the thickness of the lubricated, non-Newtonian fluid is nearly uniform, and that of the lubricating fluid is nonmonotonic with localised spikes. Despite these complex thickness patterns, lubricated GCs remain axisymmetric as long as the flux of the lubricating fluid is sufficiently smaller than the non-Newtonian fluid flux.
Related publications:
Instability of extensional flows
The interface of a fluid that displaces another fluid in a quasi-
two dimensional geometry can develop fingering patterns, which are
common to a wide range of natural systems. It is believed that
such interfaces remain stable, having planer or circular shapes,
when the displacing fluid is more viscous (less mobile). However,
some systems, such as ice sheets or squeezed pastes, develop
fingering patterns in spite of having a more viscous displacing
fluid.
We show that a more viscous displacing fluid can develop
fingering patterns if that fluid is nonlinear and is discharged
axisymmetrically along frictionless boundaries. Unlike the
classical viscous fingering, the patterns we observe resemble
tears and their characteristic wavelength progressively grows.

Related publications:

Viscous flows on porous substrate
We study the propagation of viscous gravity currents over a thin porous substrate with finite capillary entry pressure. Near the origin, where the current is deep, propagation of the current coincides with leakage through the substrate. Near the nose of the current, where the current is thin and the fluid pressure is below the capillary entry pressure, drainage is absent. Consequently the flow can be characterised by the evolution of drainage and fluid fronts. We analyze this flow using numerical and analytical techniques combined with laboratory-scale experiments. At early times, we find that the position of both fronts evolve as $t^{1/2}$, similar to an axisymmetric gravity current on an impermeable substrate. At later times, the growing effect of drainage inhibits spreading, causing the drainage front to logarithmically approach a steady position. In contrast, the asymptotic propagation of the fluid front is quasi-self-similar, having identical structure to the solution of gravity currents on an impermeable substrate, only with slowly varying fluid flux. We benchmark these theoretical results with laboratory experiments that are consistent with our modeling approximation, but that also highlight the detailed dynamics of drainage inhibited by finite capillary pressure.
Related publications:

Floating extensional flows
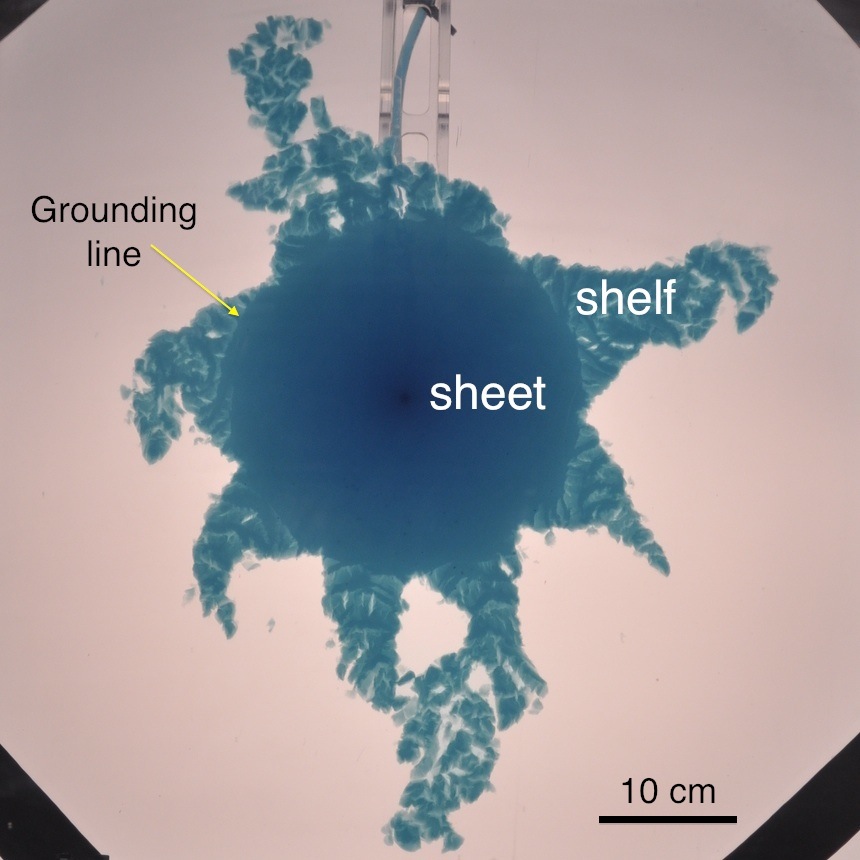 |
Ice sheets spread like viscous gravity currents into the surrounding oceans. As they spread they thin and can detach from the bed, owing to the hydrostatic pressure of the ocean, and float as ice shelves. The detachment position is a contact line that separates a grounded, shear-dominated flow and a floating, extension-dominated flow. Differences between these two flow regimes can be intensified because of the complex rheology of ice. In particular, floating shelves can fracture and potentially shatter, which may ultimately affect the stability of ice sheets and lead to a catastrophic rise in sea level. We explore fundamental aspects of this problem using laboratory experiments. We model the flow of ice sheets as viscous gravity currents that propagate in a circular geometry, and focus on the influence of the fluid rheology on the flow pattern. In particular, we study the Newtonian limit using golden syrup, and the non-Newtonian response using an aqueous suspension of Xanthan gum.
Related publications:
Axisymmetric gravity currents of power-law fluids
 |
We analyse axisymmetric gravity currents of power-law fluids theoretically and experimentally. We use aqueous suspensions of Xanthan gum in laboratory experiments of constant-volume and constant-flux release to resolve the rheological parameters of the fluid, which we then compare with measurements made using a strain-controlled rheometer. We find that the constant-volume release of highly shear-thinning fluids involves an early-time evolution dominated by inertia, and non-convex free surfaces that make the application of similarity solutions of the late-time viscously dominated evolution inefficient at resolving material properties. In contrast, constant-flux release of the same fluids can be viscously dominated and consistent with the self-similar solution from early in the evolution, which makes it a more useful method for measuring rheological parameters.
Related publications:
Elastic response of a grounded ice sheet coupled to a floating ice shelf
 |
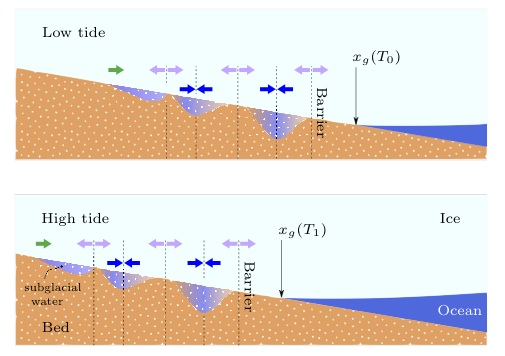
|
An ice sheet that spreads into an ocean is forced to bend owing to its buoyancy, and detaches from the bedrock to form a floating ice shelf. The location of the transition between the grounded sheet and the floating shelf, defined as the grounding-line, behaves as a free boundary. We develop a model of an elastic grounded sheet resting on a deformable elastic bed and coupled to an elastic floating shelf. We find that the grounding line position is determined by the geometry of the bed and the bending-buoyancy lengthscale of the system. These two contributions depend on the reaction modulus of the bed in opposite ways. We show that the structure of the floating shelf depends on the bending-buoyancy lengthscale only, allowing us to calculate the bending stiffness of the elastic sheet independently of the properties of the bed. Relations between the structure of the floating shelf and the grounding line position are also developed. Our theoretical predictions agree with laboratory experiments made using thick elastic sheets and a dense salt solution. Our findings may provide new insights into the dynamics near grounding lines, as well as methods to infer the bending stiffness of ice sheets and the grounding line position from satellite altimetery that can be applied to elastic sheets in general.
Related publications:
A mechanism for the spatiotemporal variability of ice streams.
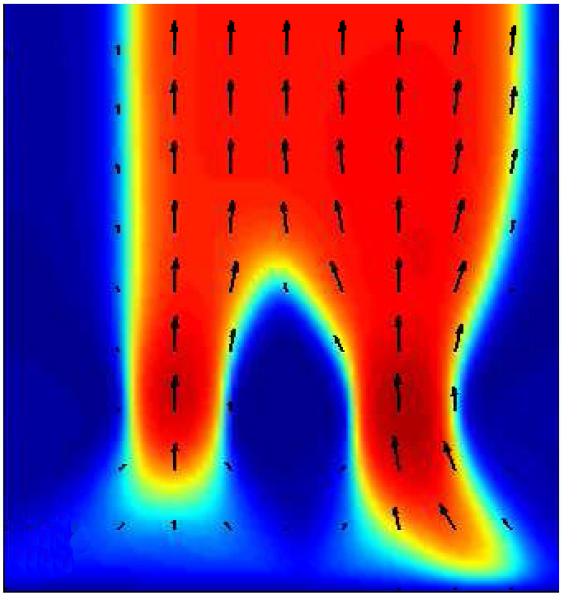 |

|
Ice streams are regions of fast flowing glacier ice that transport a
significant portion of the total ice flux from present ice sheets. The
flow pattern of ice streams can vary both temporally and spatially, in
particular, ice streams can become stagnant and change their path. We
present a mechanism that accounts for such spatiotemporal variability
of ice streams. The major element of this mechanism is a triple valued
relation between the ice velocity and the shear stress at the base of
the ice.
A triple valued sliding law was previously suggested to explain the
surging behaviour of glaciers (Fowler and Johnson, 1996). We show
that such a sliding law can be heuristically motivated by the
transverse velocity profile of an ice-stream, and use stability
analysis to explain the adjustment of the lateral shear margins to
changes in the driving stress.
We then use a 2D numerical model to demonstrate that such a sliding
law can lead to some interesting stream-like patterns and
time-oscillatory solutions. Specifically we find stable and time
oscillatory solutions of rapid stream-like regions within slow
ice-sheet flow separated by narrow shear margins. The width of those
ice streams is related to the dimensions of the mass source
distribution in the onset regions if the bed is flat, or in the
presence of a spatially uniform mass source, to the length scale
imposed by bed topography at the onset regions. This spatiotemporal
behaviour is sustained whether the ice rheology is Newtonian or
power-law viscous. We present a quantitative relation between the
parameters of the ice rheology and the width of the ice-streams
shear-margins and show how these parameters can affect the minimum
width of an ice stream before it shuts down. We then study the
interaction of two ice streams that share a common mass source and
find complex and asymmetric spatiotemporal patterns that resemble
patterns that are observed in Siple coast ice streams, Antarctica.
Related publications: A significant
portion of the ice discharge in ice sheets is drained through ice
streams, with subglacial sediment (till) acting as a
lubricant. The known importance of horizontal friction in shear
margins to ice stream dynamics suggests a critical role of
longitudinal stresses. Related publications:
Ice Streams and shear flow instability
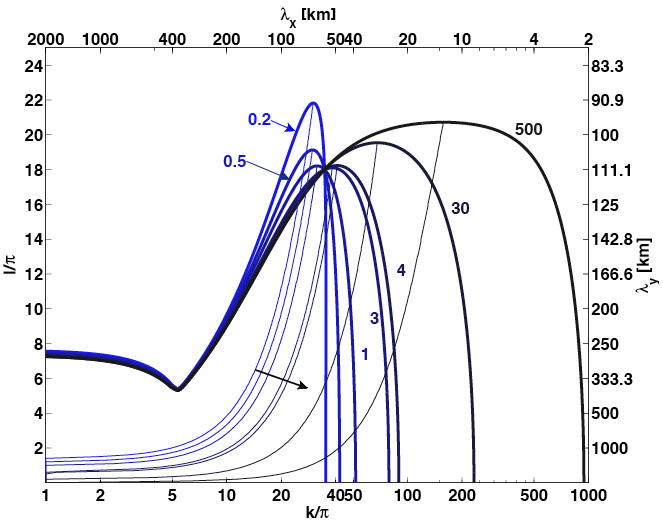
The effects of subglacial till and
longitudinal stresses on the stability of an ice sheet flow are
studied by linear stability analysis of an idealized ice-till
model in two horizontal dimensions. A power law-viscous
constitutive relation is used, explicitly including longitudinal
shear stresses. The till, which has compressible-viscous rheology,
affects the ice flow through bottom friction.
We examine the
possibility that pure ice streams develop via a spontaneous
instability of ice flow. We demonstrate that this model can be
made intrinsically unstable for a seemingly relevant range of
parameters, and that the wavelengths and growth rates that
correspond to the most unstable modes are in rough agreement with
observed pure ice streams. Instabilities occur due to basal
friction and melt water production at the ice-till interface. The
most unstable wavelength arise due to selective dissipation of
both short and long perturbation scales. Longitudinal stress
gradients stabilize short transverse wavelengths while Nye
diffusion stabilizes long transverse
wavelengths. The
selection of an intermediate unstable wave length occurs, however,
only for certain parameter and perturbation structure
choices. These results do not change qualitatively for a Newtonian
ice flow law, indicating no significant role to shear thinning,
although this may very well be due to the restrictive assumptions
of the model and analysis.