Deriving the Michaelis-Menten
Equation
This
page is originally authored by Gale Rhodes (© Jan 2000) and is still under continuous update.
The page has been substantially modified with permission by Claude Aflalo (© Jan 2000).
Memorize this
derivation as soon as your encounter it in your text, and you will be able to
read the remainder of the chapter with far greater understanding. For other
suggestions on how to make your study of biochemistry easier, see Learning Strategies.
A simple model of enzyme action:
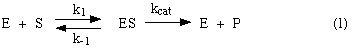
In this model, the substrate S
reversibly associates with the enzyme E in a first step, and some of the
resulting complex ES is allowed to break down and yield the product P and the
free enzyme back. We would like to know how to recognize an enzyme that behaves
according to this model. One way is to look at the enzyme's kinetic behavior --
at how substrate concentration affects its rate. So we want to know what rate
law such an enzyme would obey. If a newly discovered enzyme obeys that rate
law, then we can assume that it acts according to this model. Let's derive a
rate law from this model.
For this model, let
v0 be the initial velocity of the reaction. The latter stands for
the appearance of the product P in solution (+ d[P]/dt) whose phenomenological
rate equation (first-order) is given by
v0 = kcat[ES] (2),
containing an experimentally
measurable (dependent) variable - v0, a kinetic parameter - kcat,
and another variable unknown to us - [ES].
|
Before
proceeding, one should state (and remember) some implicite assumptions:
|
|
These
assumptions, which hold in most kinetic experiments performed in test tubes
at low enzyme concentration, are convenient when considering the mass
conservation equations for the reactants |
We want to express v0 in
terms of measurable (experimentally defined, independent) variables, like [S]
and [E]total , so we can see how to test the mechanism by
experiments in kinetics. So we must replace the unknown [ES] in (2) with
measurables.
During the initial phase of the
reaction, as long as the reaction velocity remains constant, the
reaction is in a steady state, with ES being formed and consumed at the
same rate. During this phase, the rate of formation of [ES] (one second
order kinetic step) equals its rate of consumption (two first order
kinetic steps). According to model (1),
Rate of formation of [ES] = k1[E][S].
Rate of consumption of [ES] = k-1[ES]
+ kcat [ES].
So in the steady state,
k-1[ES] + kcat[ES] = k1[E][S] (3)
Remember that we are trying to
solve for [ES] in terms of measurables, so that we can replace it in (2).
First, collect the kinetic constants, and the concentrations (variables) in
(3):
(k-1 + kcat) [ES] = k1 [E][S],and (4) (k-1 + kcat)/k1 = [E][S]/[ES]
To simplify (4), first group the
kinetic constants by defining them as Km:
Km = (k-1 + kcat)/k1 (5)
and then express [E] in terms of
[ES] and [E]total, to limit the number of unknowns:
[E] = [E]total - [ES] (6)
Substitute (5) and (6) into (4):
Km = ([E]total - [ES]) [S]/[ES] (7)
Solve (7) for [ES]:
First multiply both sides by [ES]
(no Black Magic involvement here...):
[ES] Km = [E]total[S]
- [ES][S]
Then collect terms containing [ES]
on the left:
[ES] Km + [ES][S] = [E]total[S]
Factor [ES] from the left-hand
terms:
[ES](Km + [S]) = [E]total[S]
and finally, divide both sides by
(Km + [S]):
[ES] = [E]total [S]/(Km + [S]) (8)
Substitute (8) into (2):
v0 = kcat[E]total [S]/(Km + [S]) (9)
The maximum velocity Vmax
occurs when the enzyme is saturated -- that is, when all enzyme molecules are
tied up with S, or [ES] = [E]total. Thus,
Vmax = kcat [E]total (10)
Substitute Vmax into (9)
for kcat [E]total:
v0 = Vmax [S]/(Km + [S]) (11)
This equation expresses the initial
rate of reaction in terms of a measurable quantity, the initial
substrate concentration. The two kinetic parameters, Vmax and Km
, will be different for every enzyme-substrate pair.
Equation (11), the Michaelis-Menten
equation, describes the kinetic behavior of an enzyme that acts according to
the simple model (1). Equation (11) is of the form
y = ax/(b + x) (does this look
familiar?)
This is the equation of a
rectangular hyperbola, just like the saturation equation for the binding of
oxygen to myoglobin.
Mathematically, the function v0
presents two asymptotes:
* one parallel to the [S] axis at v0
= Vmax , represents the velocity at infinite [S] (saturation),
* the second parallel to the v0 axis at [S] = - Km, has
no physical meaning (no negative concentrations).
Further analysis reveals the
physical meaning of Km: the concentration of substrate at which the
velocity is half Vmax. Indeed, substituting Km for [S] in
(11) yields
v0 = 1/2 Vmax.
Thus, a low value for Km
may indicate a high affinity of the enzyme for its substrate.
Another physically meaningful limit
of this function is found at vanishingly small values of [S] (--> 0),
where v0 --> Vmax
/Km [S].
In this case, the velocity becomes proportional to the (low, relative to Km)
substrate concentration, displaying pseudo-first order kinetics
in [S].
The parameter Vmax /Km
(or rather its constant part kcat /Km), often referred to
as the catalytic ability of the enzyme, is a direct measure of
the efficiency of the enzyme in transforming the substrate S.
kcat /Km
recombines the two traditionally-separated aspects of enzyme catalysis:
* the effectiveness of
transformation of bound product (catalysis per se, kcat )
* the effectiveness of productive substrate binding (affinity, 1/Km
= k1 /(k-1 + kcat))
Equation (11) means that, for an
enzyme acting according to the simple model (1), a plot of v0 versus
[S] will be a rectangular hyperbola. When enzymes exhibit this kinetic
behavior, unless we find other evidence to the contrary, we assume that they
act according to model (1), and call them Michaelis-Menten enzymes.
QUIZ
Quiz at first class
on enzyme kinetics: Derive equation (11) from model (1).
Ten minutes.
![]()
|
Last
update: Dec 1999- Claude
Aflalo |
You are
visitor No. |