Coherent Stern–Gerlach momentum splitting
Interferometry is a measurement technique based on the phase difference between waves. It was used already in the 17th century in order to support the claim that light is a wave and not a stream of particles. Optical interferometry is a well-established field. It uses the phase differences to measure optical length differences. On the other hand, interferometry with matter-waves is still in its infancy. Since the phase of de-Broglie waves of massive particles is extremely sensitive to forces acting on the particles, matter-wave interferometry may serve as a powerful tool for measuring potentials and forces. Interferometry is used as a sensitive tool for investigating fundamental physics (for example, testing the equivalence principle of general relativity or measuring the phase fluctuation along a 1-dimensional Bose gas) as well as for realizing technological applications (for example, measurement of linear acceleration and rotation).
In order to produce a matter-wave interferometer, the internal and external degrees of freedom of the atoms should be controlled and manipulated. This can be done with light or magnetic fields. Interferometers based on light beam-splitters put the atoms in a superposition of momentum states. Interference experiments based on magnetic field beam-splitters have been limited so far to the splitting of trapped atoms into two trapped clouds in a double-well potential. The main advantage of splitting atoms in a trap or a waveguide is the possibility of thereby controlling the motion of both outputs of the beam-splitter and manipulating each one of them independently. The atom chip is an ideal tool for precise small-scale control and manipulation using magnetic fields.
Coherent splitting on an atom chip was first realized with light. Splitting with magnetic fields was first demonstrated by the Schmiedmayer group in Heidelberg (now located in Vienna). They used a combination of a static magnetic trap and a magnetic field alternating at radio frequencies to transform a single well into a double-well potential, and to split a Bose-Einstein condensate (BEC) into two clouds. Since then, splitting of a BEC has been demonstrated on an atom chip using microwave radiation, and first indications for coherent splitting were also shown by using only static currents for the creation of the double-well potential.
In this work, which has been published in Nat. Commun. (see Papers, “Coherent Stern–Gerlach momentum splitting on an atom chip”), we choose a different approach that uses magnetic gradients for momentum splitting and combines some of the characteristics and advantages of both light and magnetic beam-splitters. This approach is inspired by the original Stern-Gerlach (SG) experiment. In the SG effect, an atom possessing a spin is exposed to a magnetic gradient and is thus accelerated in a direction which is dependent on its spin projection. If the atom is in a superposition of spin states, it will be split into different momentum states, which will transform into different paths. This idea forms the basis for the SG interferometer. Almost a century of attempts to realize this type of interferometer failed due to the high sensitivity and accuracy needed for this kind of splitting. The SG interferometer drew theoretical attention from physicists like Heisenberg, Wigner, Bohm, Lamb, and Scully, who estimated that this kind of interferometer will require such a high level of accuracy that it is impractical. By modifying the original idea, we split a BEC and showed that the two outputs of our new beam-splitter are coherent.
The physical mechanism that lies at the heart of the SG effect and of our beam-splitter is the interplay between internal spin dynamics and external motion of the atom, due to different interaction of the Zeeman sublevels with the external magnetic gradients. This mechanism was a key feature in a previous project, which studied the effect of noise on transitions between atomic levels with state-dependent potentials. The experimental configuration of this previous project is the basis for our implementation of the SG beam-splitter.
Full size image |
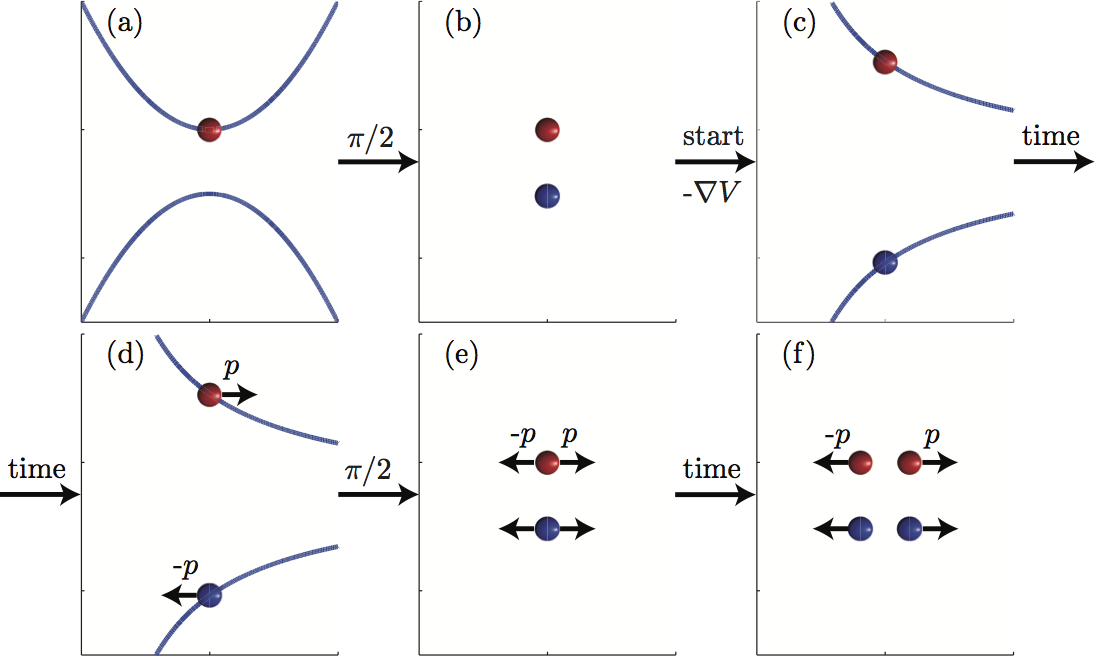
General scheme of the field gradient beam-splitter (FGBS) operation. (a) Atoms in the state |2> (red) are released from a trap. (b) A π/2 pulse splits the wave-function into a superposition of internal levels |1> (blue) and |2>. (c) A state-dependent force is applied. (d) Atoms in the two internal states are accelerated to different momenta. (e) The force is turned off and another π/2 pulse produces a superposition of 4 parts with two different momenta and two different internal states. (f) After some evolution time the momentum components are spatially separated. |
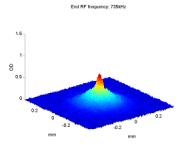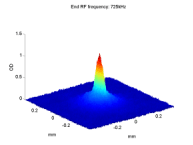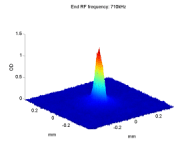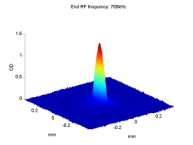
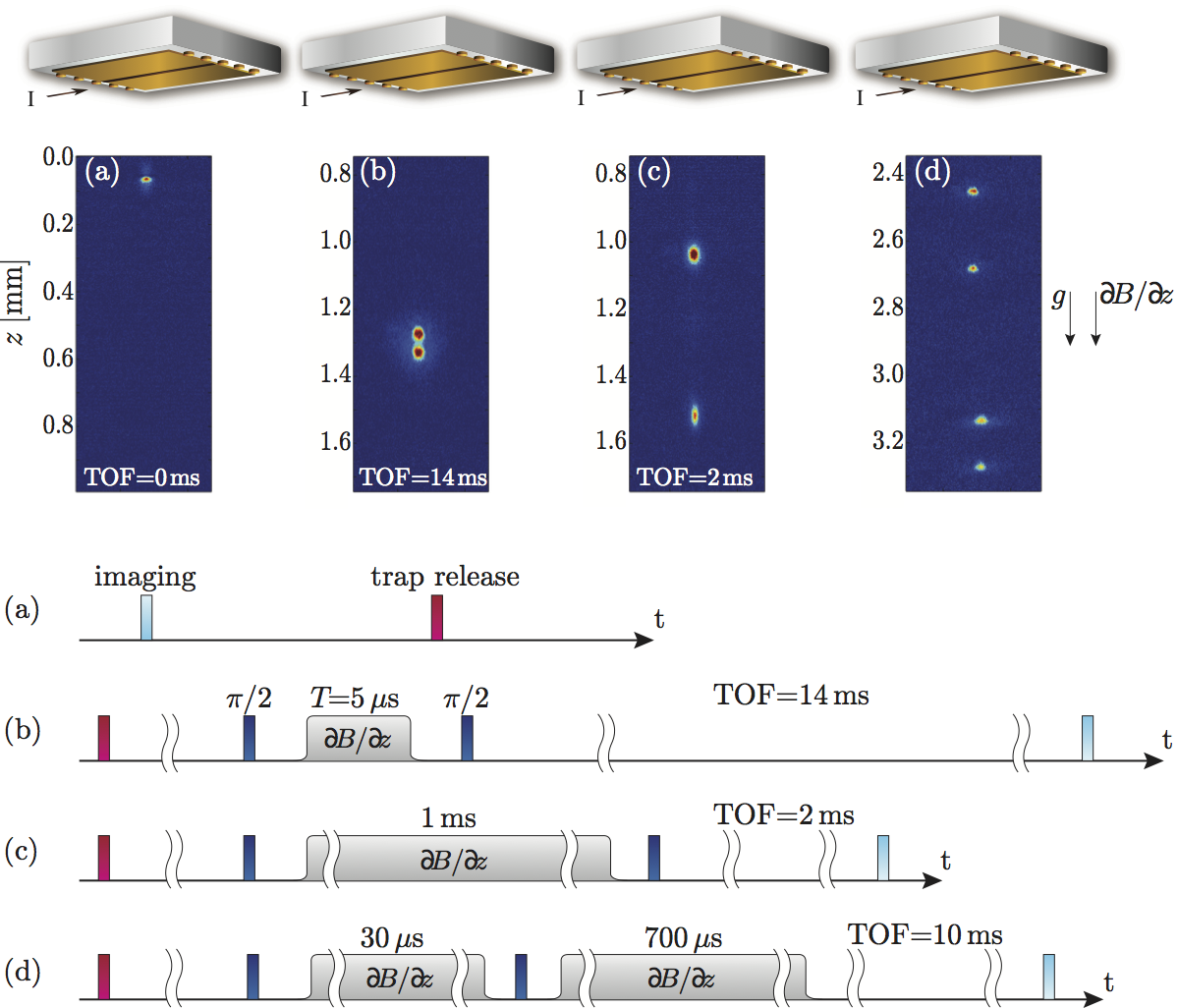
The field gradient beam-splitter at work: FGBS (a) input and (b-d) output images, and the corresponding schematic descriptions. (a) In the trap before release. (b) After a weak splitting of less than ħk using 5µs of interaction time and allowing 14ms time-of-flight (TOF). (c) After a strong splitting of more than 40ħk using 1ms interaction time and allowing 2ms TOF. (d) To view all four output wavepackets, we separate the two internal states by another strong gradient pulse. Images (b) and (c) demonstrates the large dynamic range of this method without requiring any complicated sequence. |
Full size image |
Full size image |
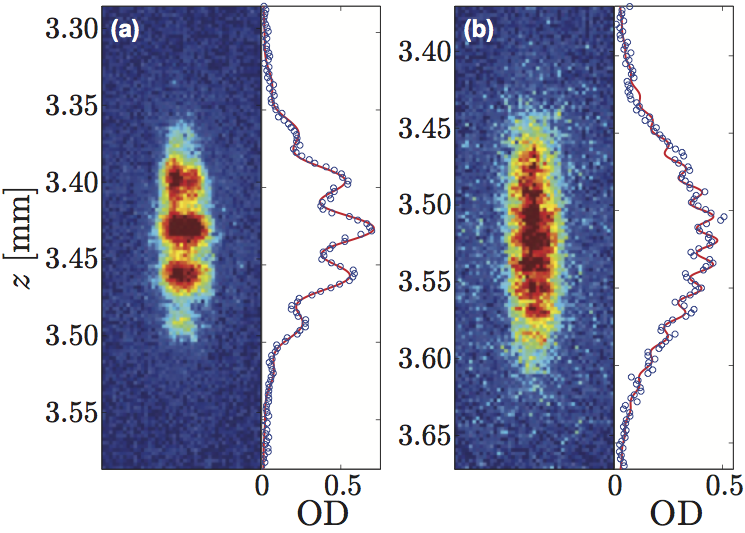
Interference fringes from freely falling atoms. Fringes for (a) short (T=5µs) and (b) long (T=10µs) interaction times, created by recombining the two outputs of the FGBS. Cuts of the optical density (OD) are also provided, with fits (see text for fit description). The two |2> wavepackets were recombined by an additional magnetic gradient and imaged after 14ms of TOF. The different T (5 and 10µs) gives rise to a different ∆v, and hence a different distance before recombination, leading to different fringe spacings, 33µm and 16µm, respectively. |
| Phase stability analysis. (a) Average over the optical densities obtained from a set of 29 consecutive single-shot images in the first half hour of an interferometric measurement session (one image per minute), and a one-dimensional cut (data and fit, see text). The visibility of the averaged fringe pattern is 0.09±0.01, reduced from the single-shot value of 0.20±0.02. The average periodicity is similar, 23.1±0.35µm in the single shots and 22.9±0.2µm in the averaged image. | 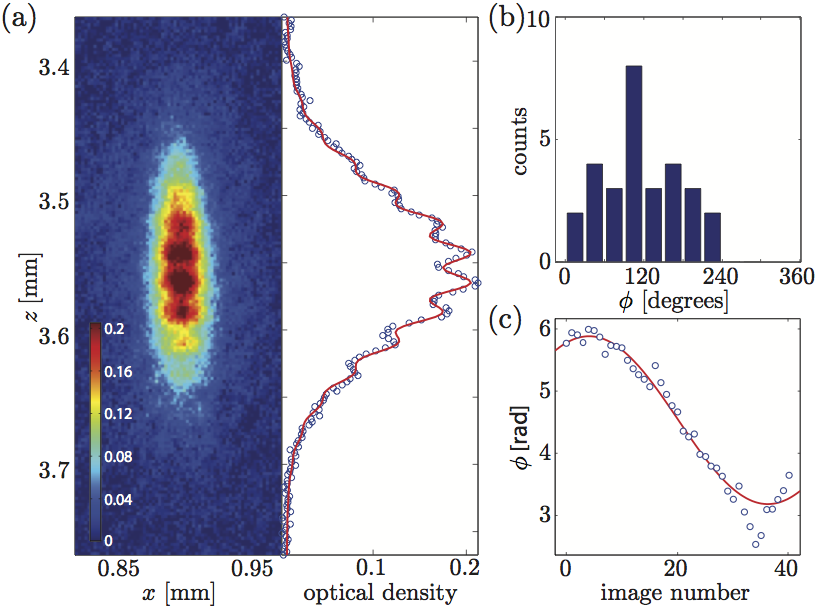
Full size image |
| (b) Phase distribution of the 29 images in π/6 radian bins, with a width of 1.04 radians (rms), in accordance with that expected by our stability analysis, see text. A random distribution has a probability of 3·(2/3)29=2.5·10-5 of similarly occupying only 2/3 of the phase spectrum. (c) Phase of fringes obtained by averaging running sets (“windows”) of 16 images for a total set of 55 consecutive images. This shows a long-term variation of the phase which is approximated by a sine fit (solid line) with an amplitude of 1.35 radian and a period of 65 minutes. The 29 images analyzed in (a) were taken near the maximum of this long-term variation. |