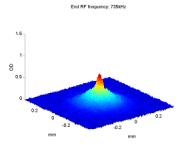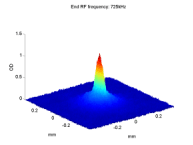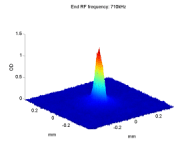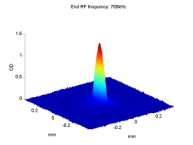
Asymmetric Transition Rates
Coupling between internal and external (motional) degrees of freedom plays a major role in cooling atoms, ions and molecules and in manipulating their quantum states, e.g., in logic gates for quantum computation. The state of these particles is usually controlled by monochromatic (or transform limited) electromagnetic fields, while incoherent fluctuations (noise) must be suppressed in order to prevent decoherence, heating and loss. The latter are usually studied under the “white noise” assumption. Little is known about what happens between the monochromatic and white noise limits (“colored noise”) with respect to control and hindering effects.
To understand how the noise spectrum can affect the rate of transitions between internal states, consider a system of two levels representing electronic configurations of an atom, ion or molecule, coupled to external (translational, rotational or vibrational) degrees of freedom and to a weak homogeneous field inducing transitions between the internal levels. If this field imposes a monochromatic perturbation, then the rate of transitions from an initial state to a final state is given by Fermi's golden rule. The transition rates are proportional to the density of states in their respective final level, and are therefore asymmetric between two levels that experience different external potentials. At the other extreme, one has a fluctuating random field with a spectral density which is flat over a large bandwidth (“white noise”). This now allows transitions to all states such that the external degrees of freedom decouple from the transition dynamics and the transition rates between the two levels become symmetric.
In this work, which has been published in PRL (see Papers, “Coupling between internal spin dynamics and external degrees of freedom in the presence of colored noise”), we study the dynamics of transitions between two internal atomic states with different external potentials in the form of two magnetically trapped Zeeman levels (|F,mF> =|2,2> and |2,1>) in the presence of colored noise which is neither monochromatic nor white. We experimentally observe that the relative transition rates between the levels strongly depend on the spectral shape of the noise. While a clear understanding of this dependence is important in order to find effective ways to combat uncontrolled noise, we demonstrate that this dependence also allows steering the transitions in the desired direction by utilizing engineered noise.
Full size image |
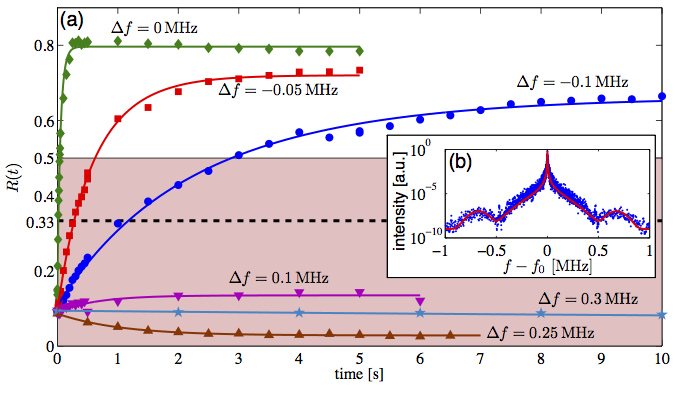
Measured ratio R(t) and the applied noise. (a) The measured ratio R(t) between the number of atoms in mF=1 and the number of atoms in both trapped levels. Different curves correspond to different values of Δf, the detuning between the noise peak frequency f0 and the Zeeman splitting E120/h between the two trapped levels at the magnetic field minimum. The measured R(t) goes beyond the |
| band 0≤R≤1/2 representing asymptotic values of R(t) in a model where the external degrees of freedom are decoupled from the transition dynamics (the dashed line at R=1/3 is for white noise). Data variance gives an error of ±0.01 (not shown). (b) The noise spectrum we introduce into the system relative to f0=18MHz (red line is the fit used in our calculations). |
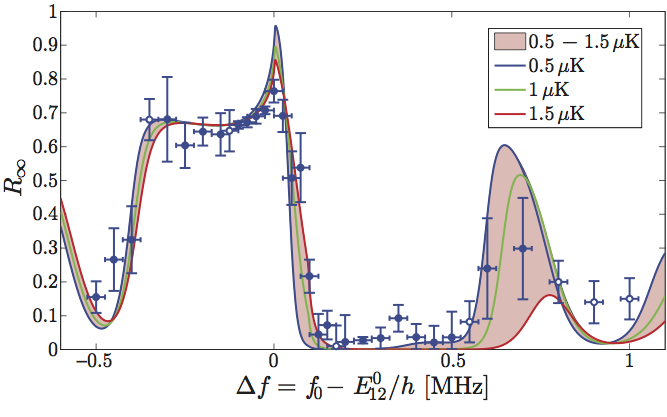
Asymptotic values R∞, as a function of Δf, compared with theory with no fitting parameters (T=0.5-1.5µK). Error bars are rms values for the data variance and mean fit error in measurements of R(t), except for open-circle data points, for which only one measurement is available and the error is the average of the entire data set. The horizontal error is the uncertainty in the magnetic field minimum. |
Full size image |
Full size image |
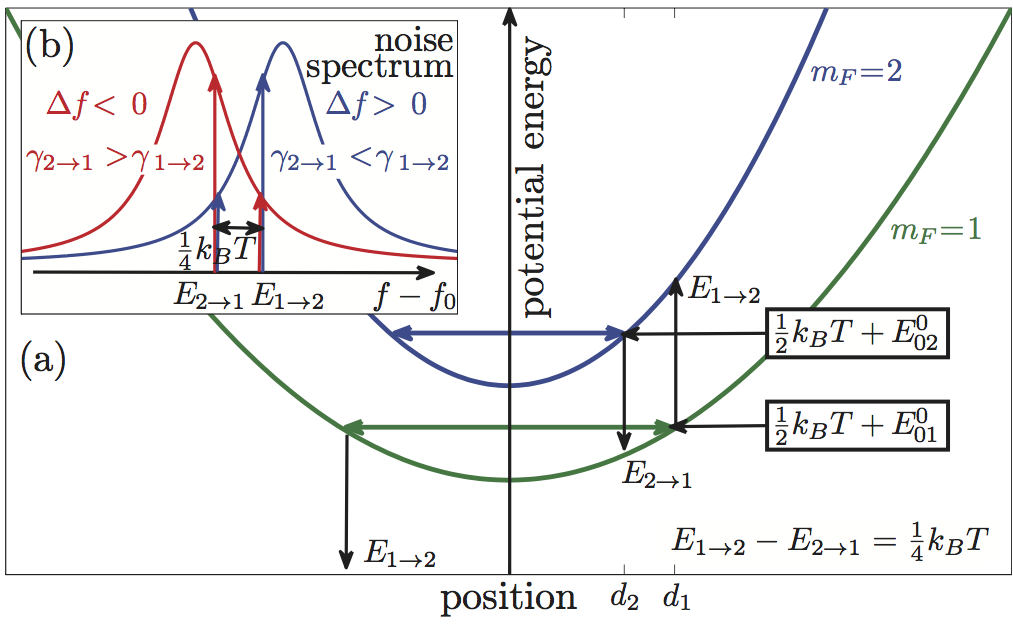
A simplified model showing the asymmetry in the transitions. (a) A simplified model showing the asymmetry in the transitions between the two trapped levels. We assume that the atoms are in thermal equilibrium at temperature T, in both levels. We plot the transitions at the mean atom distances from the trap center. A spin flip from mF=2 to mF=1 requires photon energy E2→1, which |
| is smaller than the photon energy E1→2 needed for the reverse transition. Ei→f corresponds to the difference between the potentials since the atomic recoil is negligible. (b) The two transitions sample different frequencies of the noise spectrum (plotted twice for opposite detuning), giving rise to the asymmetric transition rates. The two pairs of arrows (blue and red) point to the sampled noise intensities for each detuning. |